Strong Reducibility as an Adaptor

In the previous post, I explained how Weihrauch reducibility could be viewed as a dependent lens. That was supposed to be the start of a few blog posts because my supervisor thought this work probably wasn't publishable. However, since then, we have written this up, and a preprint is available on the Arxiv. Even better, this work was accepted for CiE, as was an abstract for TYPES. I might still write some blog posts on various container constructions, but today I want to talk about the strong (or uniform) variant of Weihrauch Reducibility.

Recall from last time that we originally defined Weihrauch reducibility by

Let $X$ , $Y$ , $Z$ , $W$ be represented spaces and let $f :\subseteq X ⇉ Y$ , $g :\subseteq Z ⇉ W$ be partial multi-valued functions. Then $f$ is Weihrauch reducible to $g$ , if there are computable partial functions $Φ, Ψ :\subseteq N^{N} \to N^{N}$ such that for all $p$ with $δ_{X} (p) \in dom (f)$ , $δ_{Z} (Φ (p)) \in dom (g)$ and for all $q$ with $δ_{W} (q) \in g (δ_{Z} (Φ (p)))$ , $δ_{Y} (Ψ (p, q)) \in f (δ_{X} (p))$ .

There is a variant of Weihrauch reducibility called “Strong Weihrauch reducibility”, which boils down to saying that our backwards map doesn't depend on the original input at all, i.e., $Ψ (-, q)$ is constant for all $q$ . However, it isn't necessarily clear to express this constraint categorically.

Fortunately, there are some very clever people at Strathclyde, particularly Jules Hedges, who explained how to do just this in a seminar talk, using what they have termed “Dependent Adaptors”.

What is a Dependent Adaptor?

Okay, slow down there. First, recall from last time that we swapped thinking about partial-multivalued functions (relations) $R \subseteq N^{N} \times N^{N}$ for thinking in terms of families ${(R_{i})}_{i \in dom (R)}$ where $R_{i} = {y | x R y}$ viewed as set bundles. This is fine™, but why not figure out what the category theory version of a relation is in the first place and use that?

Okay, what is a relation then?

If you are in a category with binary products, you might just say that a relation is a subobject or a product, but it pays to be a little more general than this and think internally. The important information about binary relations is that they have two projections and any given element of a relation depends uniquely on the result of both. Formally,

An (internal) relation from an object $X$ to an object $Y$ in a category $C$ is an object $R$ and a pair of maps $π_{X} : R \to X$ , $π_{Y} : R \to Y$ such that $π_{X}$ and $π_{Y}$ are jointly monic.

In the previous post, we also wanted to restrict to surjective functions to represent the idea that all elements of the domain should have an answer. Originally, we said that we should work with epimorphisms, but in the preprint, we changed our minds and decided we should actually have pullback-preserving epimorphisms, which were dubbed “answerable containers”. We want a similar kind of condition on our relations. In what follows, we will work in a regular category and require that $π_{Y}$ be a regular epimorphism for topology reasons.

In a regular category $C$ , an (answerable) problem $R : X \to Y$ is a relation $(R, π_{X}, π_{Y})$ such that $π_{X} : R \to X$ is a pullback-preserving epimorphism and $π_{Y} : R ↠ Y$ is a regular epimorphism.

Now, can we define adaptors?

Yes. $π_{X} : R \to X$ gives us the same data as we had last time, so we can carry over part of our definition of reducibility as before, but now we need to extend our diagram in the opposite direction to account for the extra regular epimorphism $π_{Y}$ .

Given problems 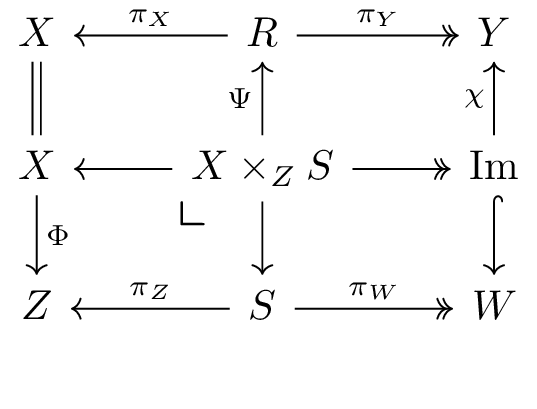$R : X \to Y$ , $S : W \to Z$ in $Pasm (K_{2}^{rec}, K_{2})$ . Then $R$ is strongly Weihrauch Reducible, $R \leq_{S W} S$ , if there exists arrows $Φ : X \to Z$ , $Ψ : X \times_{Z} S \to Y$ , $χ : Im \to Y$ such that the following diagram commutes Commuting Diagram for adaptors

Note that the arrows $X \times_{Z} S ↠ Im ↪ Z$ come from the (regular-epi, mono)-factorisation in a regular category.

The data $(Φ, Ψ, χ)$ that witnesses a reduction is known as a dependent adaptor.

To see that this is the right definition, we will need to do some unpacking. Just as last time, we will view the problem (relation) as the type $R = \sum_{x : X} Y (x)$ with the obvious projections and similarly for $S$ . Leveraging the work from last time, the left-hand side of the diagram already gives us a regular Weihrauch reduction between $π_{X} : R \to X$ and $π_{Y} : S \to Z$ . So, what is $Im$ ? We want to factor the map $X \times_{W} S \to S ↠ W$ through its image, so let's figure out what that map should do first. From last time, we know that the pullback in the centre is $\sum_{x : X} W (Φ (x))$ , so the composite map must take $(x, w)$ to $w$ , where $x \in X$ and $w \in W (Φ (x))$ , and hence the image must be the union of all $W (Φ (x))$ .

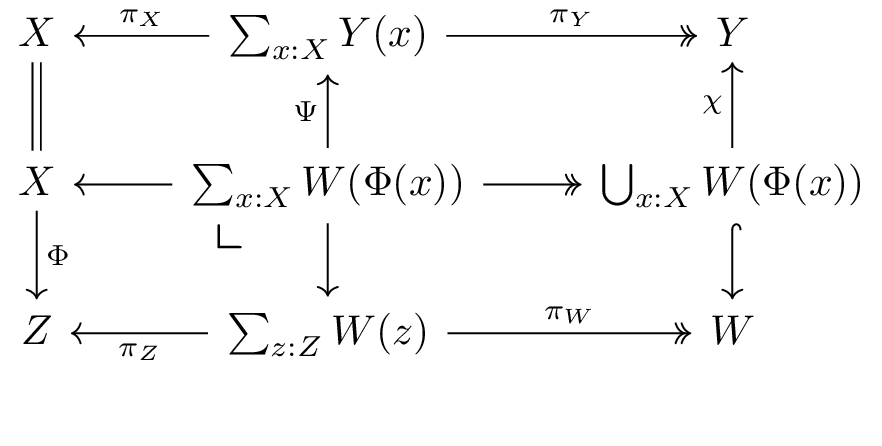
Commuting Diagram for adaptors in the special case of the previous paragraph

The top left rectangle gives the equality $Ψ (x, w) = χ (w)$ for all $x \in X$ and $w \in W (x)$ . In other words, $Ψ (-, w)$ is constant, which is what we wanted.

More formally, we can say we have a full & faithful functor from strong reductions to dependent adaptors and it wouldn't take much more work to get an equivalence.

The Strong Weihrauch degrees are isomorphic to the posetal reflection of the category of answerable containers and dependent adaptors over the category of projective represented spaces and (type 2) computable functions.

Is there a pattern to the definitions?

This is a very astute question. I will defer a full post on this for another day, but the short answer is that lenses come about as a result of taking the opposite of a fibration, see e.g. Streicher (Section 5). You can see this at play in papers like Spivak's. In this view, dependent lenses arise as the opposite of the codomain fibration and dependent adaptors from the fibration $X \leftarrow R ↠ Y \mapsto X$ .

That's all folks. I have two other posts half-written, and at some point will talk about the work on fixed points I've been doing with my supervisor.